1220
자료구조 객관식, 알고리즘 주관식
시험문제
알고리즘 수행시간 비교 안나옴 빅오는 안봐도 될듯
알고리즘 이론, 빈칸채우기, 쉘,퀵,힙 정렬 <- 이론적으로 외워둬야됨
기초정렬은 소스코드 빈칸채우기
이진탐색트리는 이론과 소스코드 둘다 외워두기
이진탐색트리와 균형이진탐색 트리를 나눠서 공부하기 <- 특정 키값을 삭제 후 어떻게 되는지
균형이진탐색트리 - 삽입,삭제 연산, 특히 삭제 연산할때 자식 노드의 갯수에 따라 달라지는거 주의깊게 보기
균형이진탐색트리는 이론과 동작 방식, 삽입 삭제 어떻게 변화하는지, avl은 균형잡는 거 위주로 물어본다
이진탐색트리 - 이론, 알고리즘 둘다 , 삭제연산
균형이진탐색트리 트리 삽입, 삭제 둘다 물어본다, 삭제 후 균형잡기 - 그렇게 빡세게 물어보진 않는다
쉘정렬
삽입정렬에 전처리 과정을 추가해서 한 자리씩 이동하는 삽입정렬과 다르게 일정 간격으로 떨어진 원소들 끼리 삽입정렬을 수행한다, 리스트를 간격을 줄여가면서 정렬하고 간격이 1인 경우에는 삽입 정렬과 동일하다
부분 리스트가 점전적으로 정렬된 상태에서 삽입정렬을 하기에 속도가 증가한다
def shell_sort(a) :
n = len(a)
gap = n // 2
while gap >= 1 :
if (gap % 2) == 0 : gap += 1
for i in range(gap, n) :
j=i
while j >= gap and a[ j] < a[ j-gap]: #삽입 위치를 찾음
a[ j], a[ j-gap] = a[ j-gap], a[ j] #항목 이동
j -= gap
print(' Gap =', gap, a)
gap = gap//2
data = [5, 3, 8, 4, 9, 1, 6, 2, 7]
print("Original :", data)
shell_sort(data)
print(" Shell :", data)
힙정렬 (파이썬의 힙은 최소힙이다)
힙정렬은 이진힙을 이용해서 하는 정렬이다
완전이진트리 : 모든 레벨의 노드가 채워져있고 마지막 레벨은 왼쪽부터 차있어야 한다
이진힙 : 완전이진트리 + 부모의 우선순위가 자식의 우선순위보다 높음
최대힙 : 내림차순, 최소힙 : 오름차순
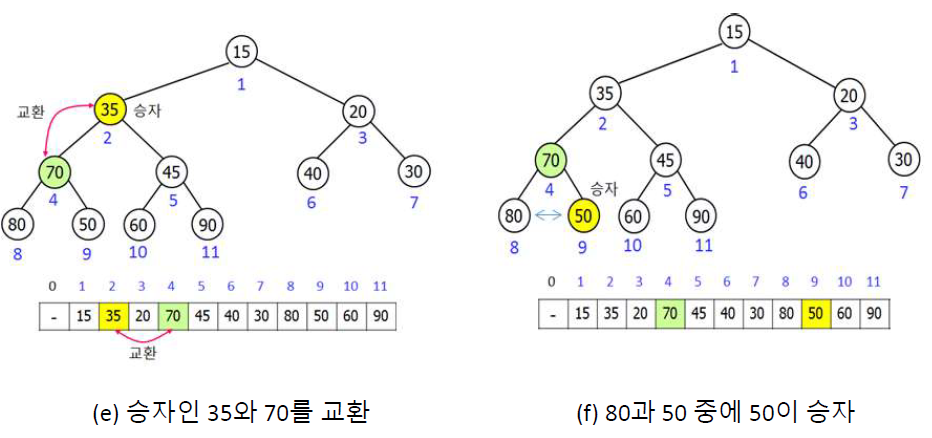
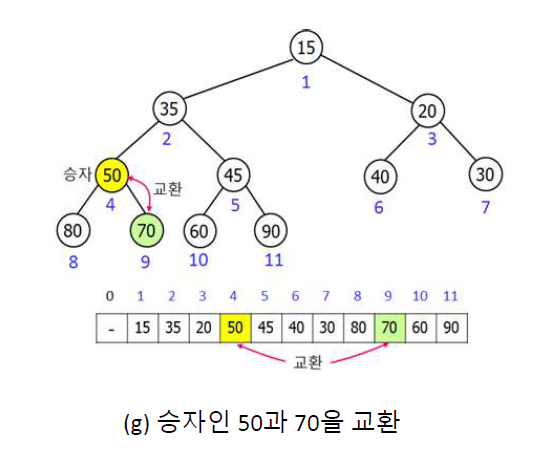
최대힙을 유지하는 방법
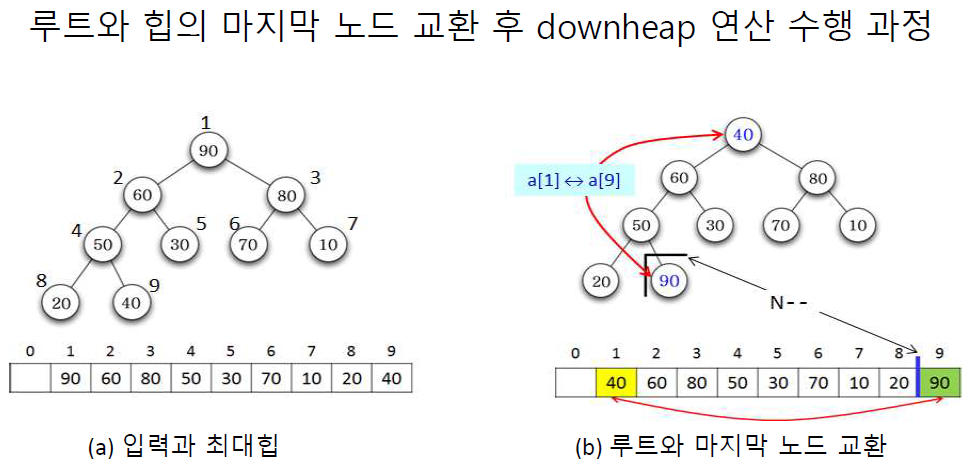
루트와 힙의 마지막 노드를 교환한 후 downheap 연산을 수행한다
루트와 마지막 노드를 교환한 힙의 크기를 1줄이고(최대힙이라 루트가 항상 크다, 교환한 루트는 더 이상 비교할 필요 X)
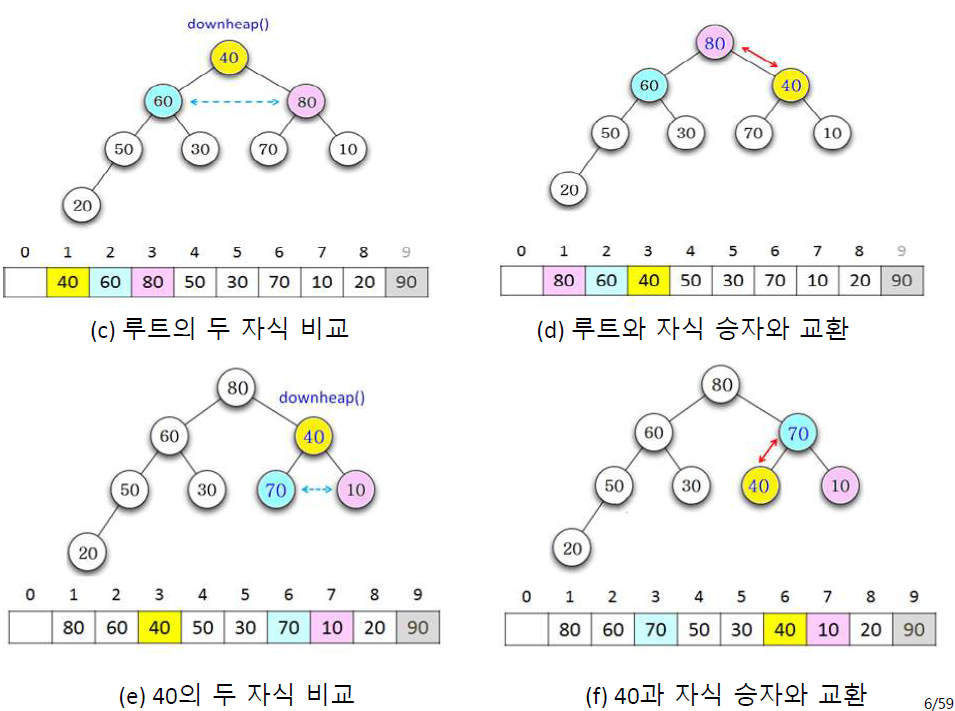
교환된 루트부터 두 자식을 비교해서 승자가 된 자식을 루트와 교환하고 다시 교환된 루트를 승자의 자식들과 비교하는
연산을 루트가 더 클때까지 반복한다.
이 downheap 연산을 2번해서 힙속성을 충족시키고 위 과정을 힙 크기가 1이 될 때까지 반복한다
힙 정렬에서 최소값 삭제
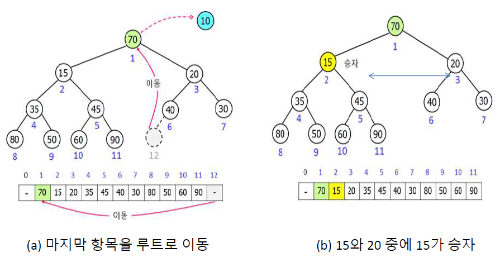
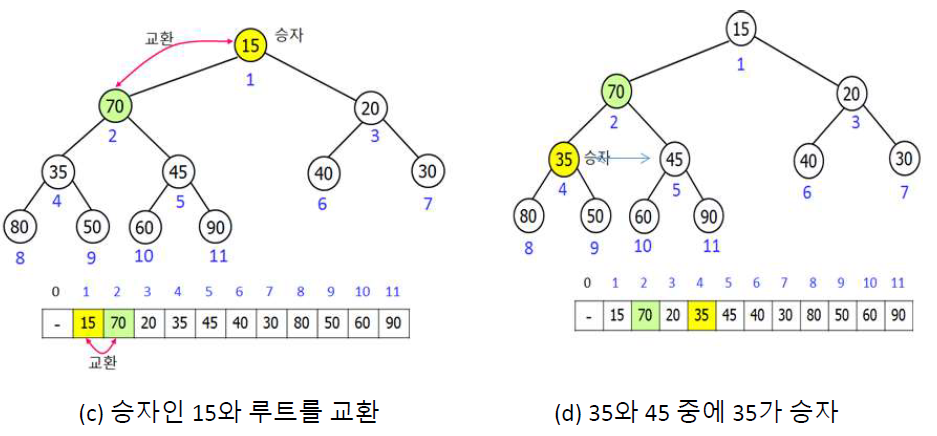
힙의 마지막 노드를 루트로 옮기고 힙의 크기를 1 감소, 루트부터 승자(더 작은 값을 가진 자식)을 찾아서
힙속성을 만족할 때 까지 키를 교환한다
힙 정렬에서 삽입 연산
마지막 노드의 바로 다음에 새 항목을 저장하고
루트 방향으로 힙 속성을 만족할 때 까지 노드를 교환하면서 올라간다(upheap)
- 마지막에 삽입 후 부모와 비교하는 연산을 계속 수행한다
힙정렬 전체 코드
def downheap(i, size):
while i*2 <= size:
k = 2*i
if k < size and a[k] < a[k+1]:
k += 1
if a[i] >= a[k]:
break
a[i], a[k] = a[k], a[i]
i = k
def create_heap(a):
hsize = len(a) - 1
# 힙 크기의 절반 + 1 까지만 down힙을 하는 이유 n//2 +1 부터 n 까지의 노드는 리프 노드라 자체로 최소 힙이기 때문이다
for i in reversed(range(1, hsize // 2 +1)):
downheap(i, hsize)
def heap_sort(a):
n = len(a) -1
for i in range(n):
a[1], a[n] = a[n], a[1]
downheap(1, n-1)
print(f"sept{i} = ", a)
n -= 1
a = [0,24, 17, 33, 50, 60, 70]
print('정렬 전 \t', end = '')
print(a[1:])
create_heap(a)
print('최대 힙 \t', end = '')
print(a[1:])
heap_sort(a)
print('정렬 후 \t', end = '')
print(a[1:])! 시험에 나올거 같음
create_heap을 할때 범위가 a[N//2+1]∼a[N]에 대하여 downheap을 수행하지 않는 이유는
위 범위의 노드들은 리프 노드라 각 노드가 힙의 크기가 1인 최소힙이기에 downheap을 수행하지 않는다
퀵 정렬
피벗을 설정하고 피벗을 기준으로 리스트를 2개의 부분리스트로 분할해서 다시 퀵 정렬을 하는 재귀 알고리즘 이다
진행 방식을 잘 외워두자

def quick_sort(a,left,right):
if left < right:
q = partition(a, left, right)
quick_sort(a,left,q-1)
quick_sort(a, q+1, right)
def partition(a, left, right):
low = left + 1
high = right
pivot = a[left]
while(low <= high) :
while low <= right and a[low] < pivot : low += 1
while high >= left and a[high] > pivot : high -= 1
if low <= high : #교차됬을때 두 레코드 교환
a[low], a[high] = a[high], a[low]
low, high = low + 1, high -1
a[left], a[high] = a[high], a[left] # 마지막으로 high와 피벗 위치 교환
return high
a = [24, 17, 33, 55, 16, 2]
print('정렬 전 \t', end = '')
print(a)
quick_sort(a,0,len(a)-1)
print('정렬 후 \t', end = '')
print(a)
순차 탐색 - 앞에서부터 뒤로 쭉 이동하면서 탐색한다, 성공시 인덱스 반환, 실패시 none 반환
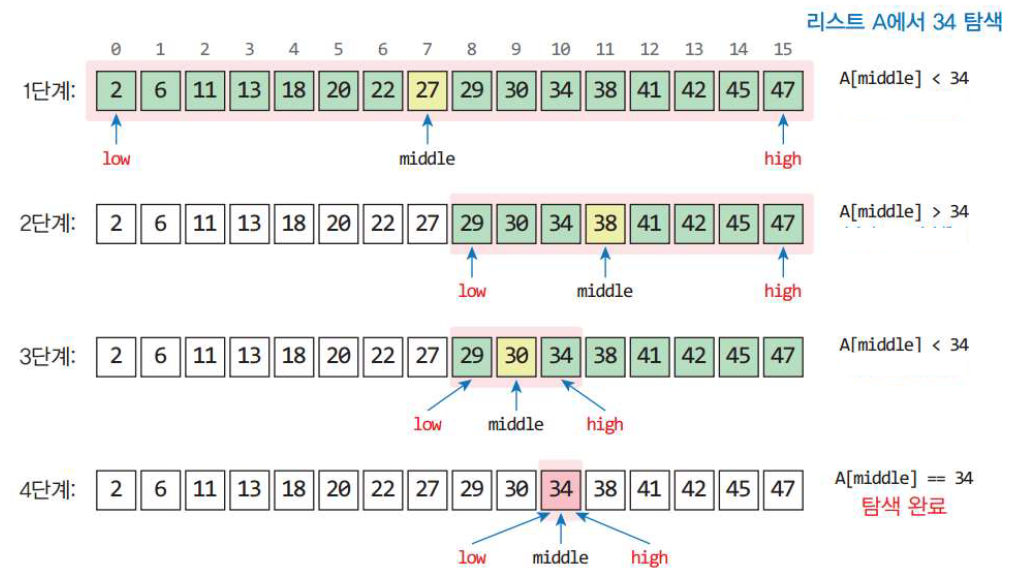
이진탐색
* 정렬된 배열을 탐색한다
배열 중앙 값이 찾고자 하는 값이 아니면 탐색 범위를 중앙 기준 왼쪽인지 오른쪽인지를 찾아서 탐색의 범위를 줄여가면서 탐색한다
def binary_search(a, key, low, high):
if(low <= high):
middle = (low + high) // 2
if key == a[middle]:
return middle
elif (key < a[middle]):
return binary_search(a,key,low,middle-1)
else:
return binary_search(a,key,middle+1,high)
return None # 탐색 실패
a = [5, 8, 15, 20, 25, 30]
print(binary_search(a, 30, 0,len(a)-1))
이진탐색트리
이진탐색트리의 특징 - 트리를 중위순회하면 정렬되어서 출력
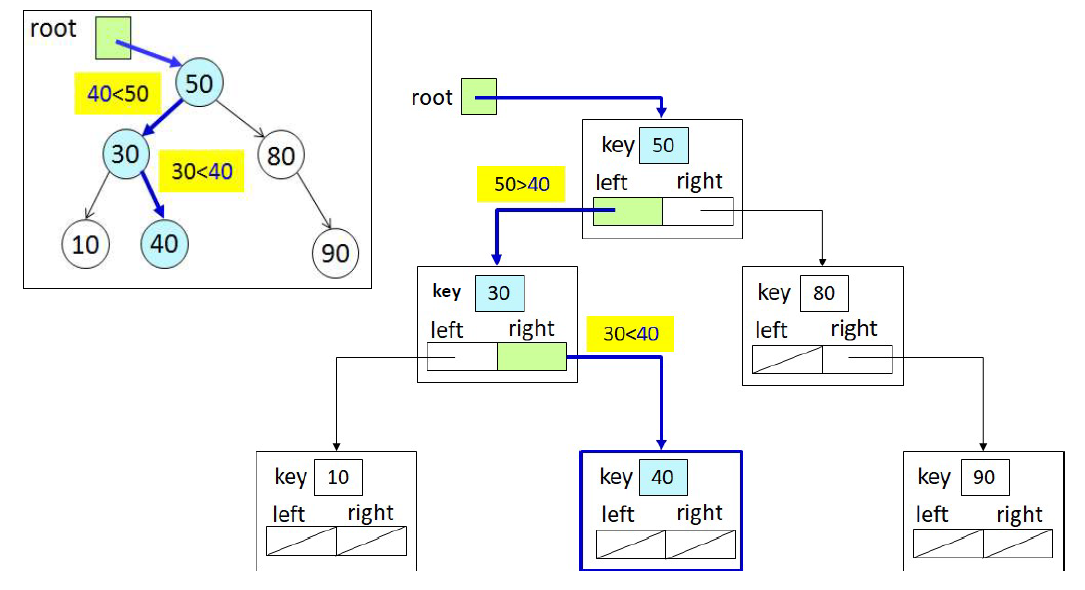
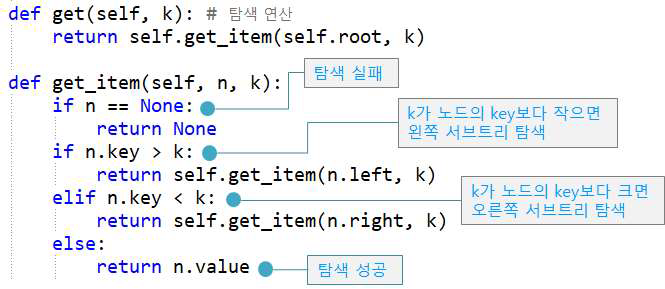
이진탐색트리 탐색 연산
탐색하고자 하는 키가 k라면, 루트의 키와 k를 비교하는 것으로 탐색을 시작
루트의 키가 k 보다 크면, 루트의 왼쪽 서브트리에서 k를 찾고,작으면 루트의 오른쪽 서브트리에서 k를 찾으며
k와 키값이 같으면 탐색 성공
왼쪽이나 오른쪽 서브트리에서 k의 탐색은 루트에서의 탐색과 같은 과정으로 이루어진다
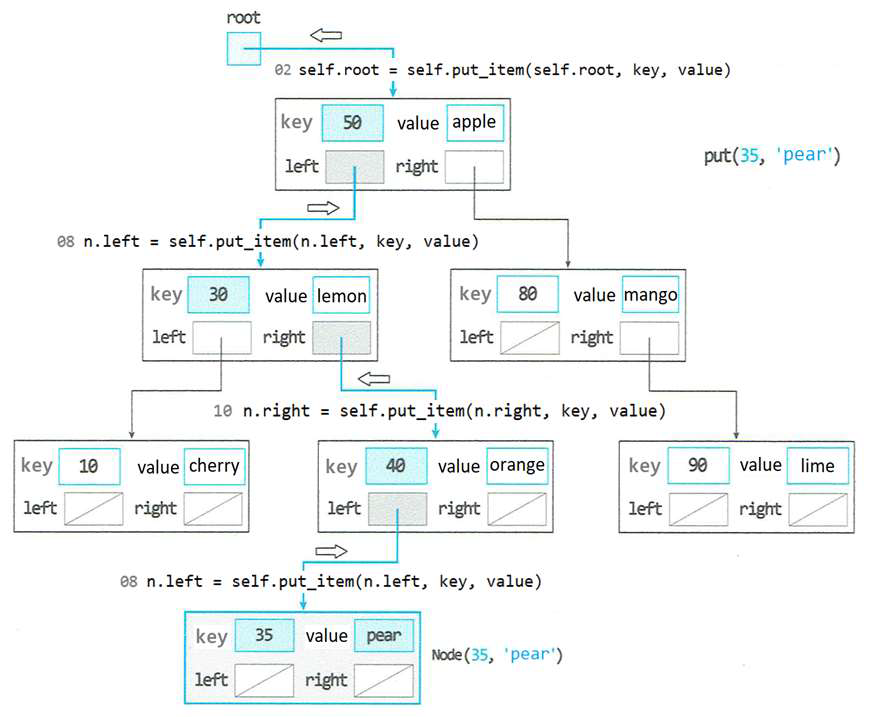
이진탐색트리 삽입 연산
탐색 중 None을 만나면 새 노드를 생성하여 부모노드와 연결
단, 이미 트리에 존재하는 키를 삽입한 경우, value만 갱신
삽입 후에는 거슬러 올라가면서 다시 이진탐색트리에 연결한다

이진탐색트리 최소값 찾기
최솟값은 루트노드로부터 왼쪽 자식을 따라 내려가며(왼쪽 자식을 따라 내려가는 이유는 왼쪽이 더 작은 자식이기 때문)
None을 만났을때 None의 부모가 가진 value

! 이진탐색트리 최소값 삭제후 연결 <- 시험에 나올 가능성이 높다
최솟값을 가진 노드 n을 찾아낸 뒤, n의 부모 p와 n의 오른쪽 자식 c를 연결한다
c가 None 이더라도 자식으로 연결한다
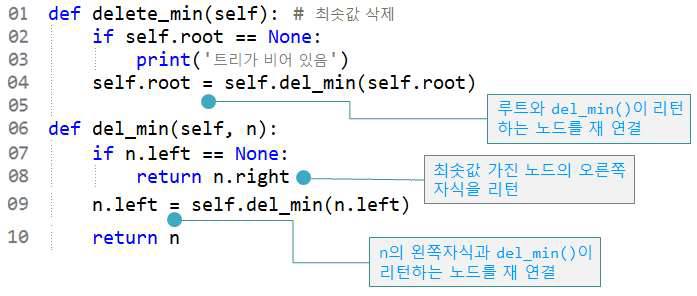
호출하는 함수인 delete_min에서는 루트에 del_min에서 리턴하는 노드를 연결한다
del_min 함수에서는 왼쪽 노드가 비었으면 오른쪽 노드를 리턴하고
아니면 왼쪽 노드에 del_min이 리턴하는 노드를 재연결한다
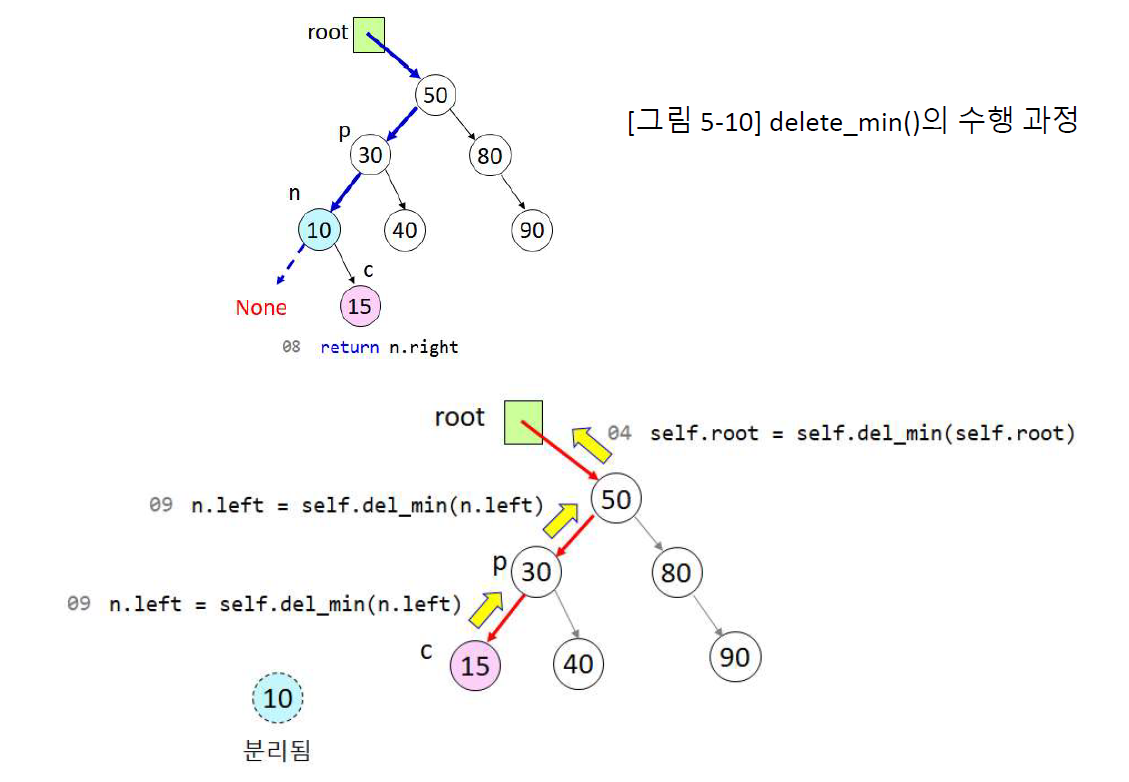
10까지 왼쪽노드를 타고 온 다음 10의 왼쪽 노드가 없으니 오른쪽 노드인 15를 리턴하고 다시 재귀를 빠져나가 거슬러
올라가면서 15가 왼쪽 노드로 이동해 키값이 10인 노드의 자리에 들어가고 제일 작은 값인 10이 분리된다
!이진 탐색트리 삭제 연산 <- 시험에 나올 가능성 매우 높다
우선 삭제하고자 하는 노드를 찾은 후 이진탐색트리 조건을 만족하도록 삭제된 노드의 부모와 자식(들)을 연결
삭제되는 노드가 자식이 없는 경우,자식이 하나인 경우, 자식이 둘인 경우로 나누어 delete 연산을 수행
삭제되는 노드 n의 자식이 없는 경우엔 부모가 n을 가리키는 것을 None으로 만든다
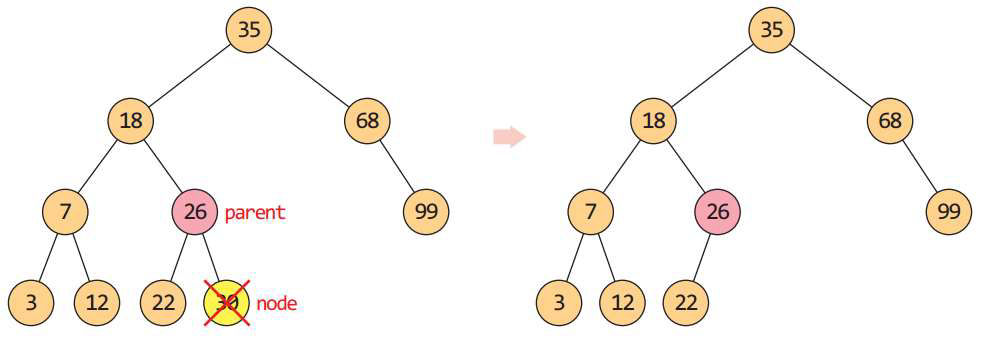
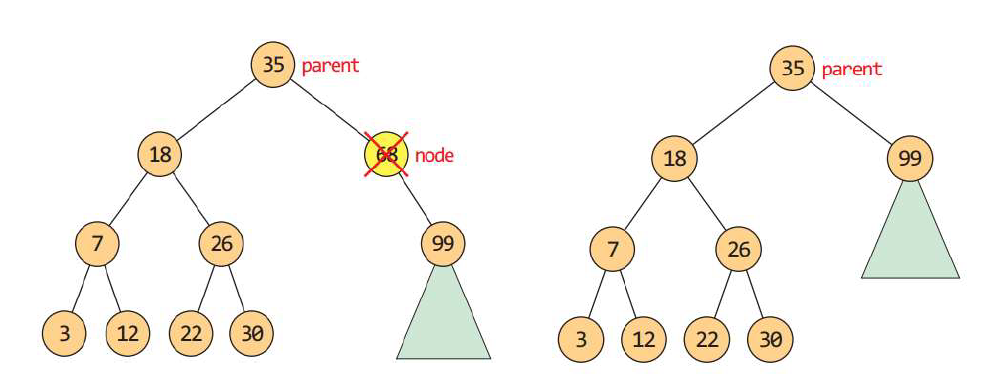
삭제되는 n이 한쪽 자식인 c만 가지고 있다면, n의 부모와 n의 자식 c를 연결해서 n을 c가 대체한다
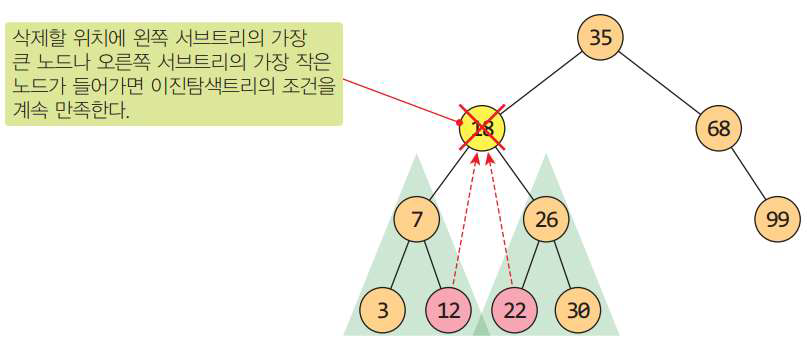
삭제될 노드 n이 자식을 두개 가지고 있다면 n의 자리에 n의 왼쪽 서브트리에서 가장 큰 노드나 n의 오른쪽 서브트리에서 가장 작은 노드를 넣어서 이진탐색트리의 조건을 계속 만족하게 한다
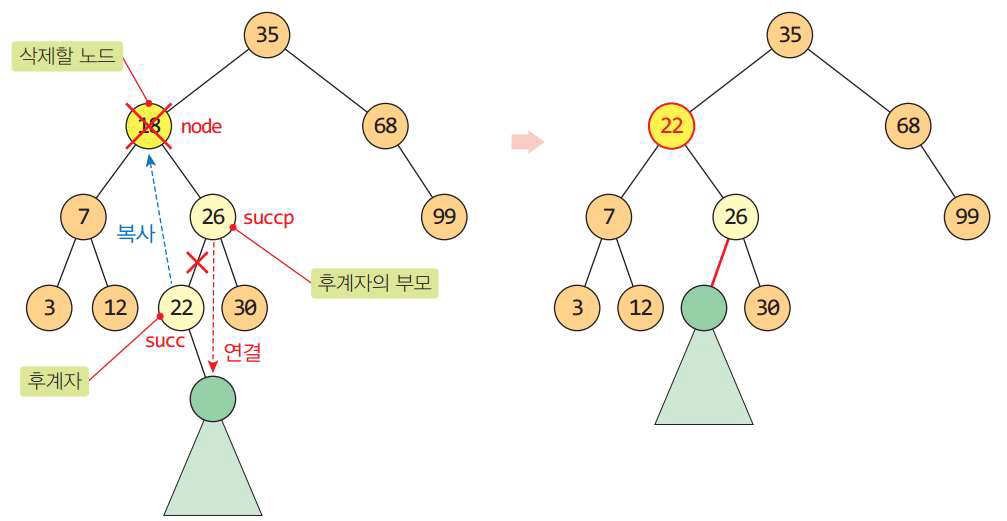
교재에서는 타겟 노드의 오른쪽 노드중 제일 작은 노드를 찾아서 대체하게 했다

전체 코오드
class Node:
def __init__(self, key, value, left = None, right = None):
self.key = key
self.value = value
self.left = left
self.right = right
class BST:
def __init__(self):
self.root = None
#탐색연산
def get(self, k):
return self.get_item(self.root, k)
def get_item(self, node, k):
if node == None: #탐색 실패
return None
if node.key > k:
return self.get_item(node.left, k)
elif node.key < k:
return self.get_item(node.right, k)
else:
return node.value
#삽입연산
def put(self, key, value):
self.root = self.put_item(self.root, key, value)
def put_item(self, node, key, value):
#n번째 노드가 없으면 생성
if node == None:
return Node(key,value)
# n번째 노드의 키값이
if node.key > key:
node.left = self.put_item(node.left, key, value)
elif node.key < key:
node.right = self.put_item(node.right, key, value)
#기존에 해당 키 값이 있으므로 값을 갱신
else:
node.value = value
return node
#최소값 찾기, delete 연산에서 사용됨
def min(self):
if self.root == None:
return None
return self.minimum(self.root)
def minimum(self, node):
if node.left == None:
return node
return self.minimum(node.left)
def delete_min(self):
if self.root == None:
print('트리가 비었음')
self.root = self.del_min(self.root)
#최소값 삭제 연산
def del_min(self, node):
if node.left == None:
return node.right
node.left = self.del_min(node.left)
return node
#삭제 연산
def delete(self, k):
self.root = self.del_node(self.root,k)
def del_node(self, node, k):
if node == None:
return None
if node.key > k :
node.left = self.del_node(node.left, k)
elif node.key < k:
node.right = self.del_node(node.right, k)
else:
if node.right == None:
return node.left
if node.left == None:
return node.right
target = node #삭제될 노드
node = self.minimum(target.right)
node.right = self.del_min(target.right)
node.left = target.left
return node
def preorder(self, node):
if node == None:
return
else:
print(node.key, end =' ')
self.preorder(node.left)
self.preorder(node.right)
def inorder(self, node):
if node == None:
return
else:
self.inorder(node.left)
print(node.key, end =' ')
self.inorder(node.right)
bst = BST()
bst.put(50,1)
bst.put(80,1)
bst.put(30,1)
bst.put(10,1)
bst.put(40,1)
bst.put(90,1)
bst.put(15,1)
bst.inorder(bst.root)
print()
print(bst.delete(10))
bst.inorder(bst.root)
print()균형이진탐색트리
균형이진탐색트리 핵심 : AVL트리는 삽입이나 삭제로 인해 균형이 깨지면 회전연산을 통해 트리의 균형을 유지한다
AVL트리는 임의의 노드 x에 대해 x의 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1을 넘지 않는다
A(3) = 4인 이유
높이가 3인 AVL 트리에는 루트와 루트의 왼쪽 서브트리와 오른쪽 서브트리가 존재해야 하고
각 서브트리 역시 최소 노드 수를 가진 AVL 트리여야 하므로
또한 이 두 개의 서브트리의 높이 차이가 1일 때 전체 트리의 노드
수가 최소가 되기 때문
노드높이 구하기 : 말단은 0, 아닌경우 좌우 높이중 높은거에 +1
AVL 균형 인수 : 왼쪽서브트리 높이 - 오른쪽서브트리 높이
균형인수가 1,0,-1을 벗어나면 avl 트리가 깨진다 1 <- 왼쪽으로 치우침, 0 <- 균형, -1 <- 오른쪽으로 치우침

AVL트리 탐색연산 - 이진탐색트리와 동일하다
AVL트리의 삽입, 삭제연산시 AVL트리의 균형이 깨질 수 있다
AVL 트리의 삽입 연산
삽입 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수에 영향을 미친다
삽입 후에 불균형 상태로 변한 가장 가까운 조상 노드(균형 인수가 ±2가 된 가장 가까운 조상 노드)의 서브 트리들에 대하여 다시 재균형
삽입 노드부터 균형 인수가 ±2가 된 가장 가까운 조상 노드까지 회전한다
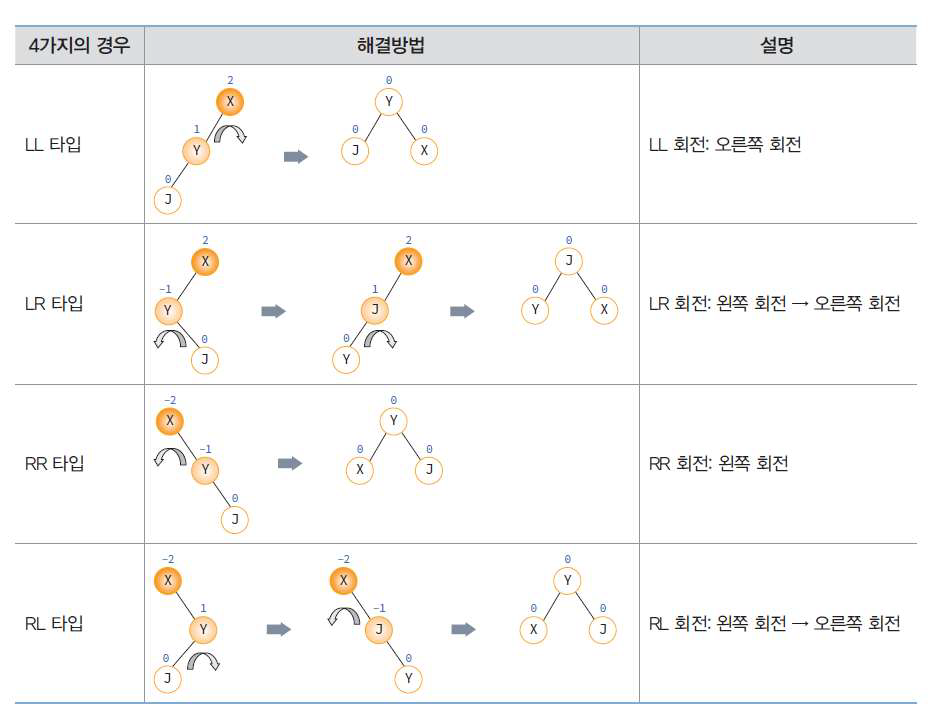
균형이 깨지는 4가지 경우
– LL, LR, RL, RR 타입
삽입된 노드 N으로부터 가장 가까우면서 균형 인수가 ±2가 된
조상 노드가 A라면
– LL 타입: N이 A의 왼쪽서브트리의 왼쪽서브트리에 삽입
– LR 타입: N이 A의 왼쪽서브트리의 오른쪽서브트리에 삽입
– RR 타입: N이 A의 오른쪽서브트리의 오른쪽서브트리에 삽입
– RL 타입: N이 A의 오른쪽서브트리의 왼쪽서브트리에 삽입
• 각 타입별 재균형 방법
– LL 회전: A부터 N까지의 경로상 노드의 오른쪽 회전
– LR 회전: A부터 N까지의 경로상 노드의 왼쪽-오른쪽 회전
– RR 회전: A부터 N까지의 경로상 노드의 왼쪽 회전
– RL 회전: A부터 N까지의 경로상 노드의 오른쪽-왼쪽 회전

강의 보고난 후에 이어서 작성하기


