기술면접 스터디 선형 자료구조 준비 자료

출처 - https://www.geeksforgeeks.org/introduction-to-linear-data-structures/?ref=lbp 

Introduction to Linear Data Structures - GeeksforGeeks

배열 - 인접한 메모리 위치에 있는 동일한 타입의 데이터의 모음

순차적인 메모리에 위치한 정적 배열

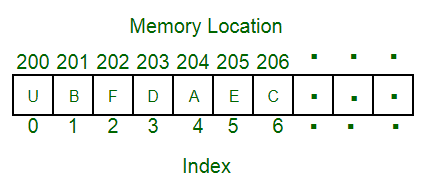
장점

인덱스 접근에 O(1)랜덤 액세스가 가능

단점

정적 메모리 크기 변경 불가능

중간 삽입/삭제시 삽입 요소 이후 요소들을 이동시키기에 O(n)의 시간 소요

 

순차적인 데이터, 사이즈 변경이나 삽입 삭제가 잦지 않은 데이터에서 사용

ex) 주식 차트,  데이터베이스 레코드 

 

배열 데이터 구조는 연결된 목록, 스택, 큐, 트리, 그래프 등과 같은 다른 데이터 구조를 구현하는 데 사용

 

동적 배열(vector, arraylist) 
실행 시간에 힙 영역에 크기를 할당하는 동적 배열,

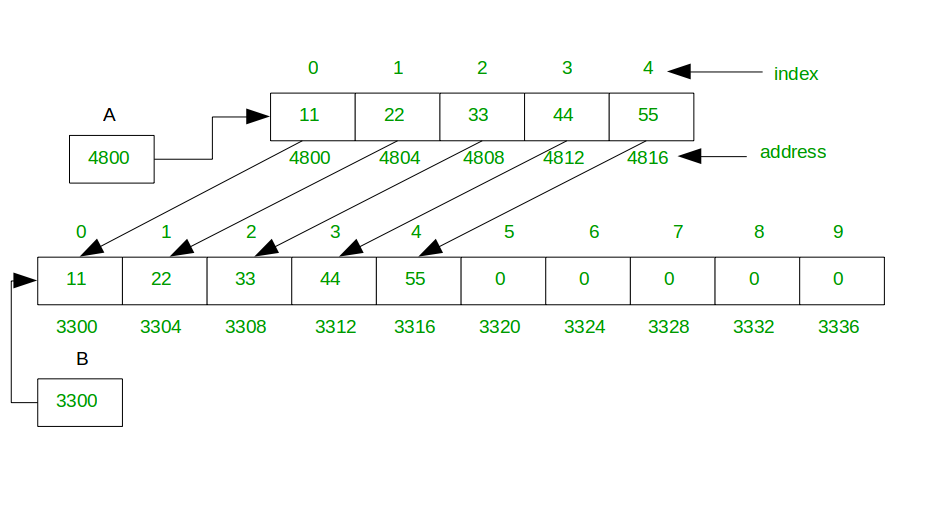
동적 배열 구조

배열 확장

배열이 꽉차면 2배로 크기를 증가시키고, 기존 배열을 복사 후 요소추가, 기존배열을 삭제 하는 방식으로 배열 확장

 

배열 축소

배열에서 요소를 삭제시 마지막 요소를 초기화하고 사이즈를 1줄임, 배열 크기가 원래 크기의 절반이 되었으면 크기가 절반인 배열을 선언하고 복사, 기존 배열을 삭제하는 식으로 메모리 관리 

 

중간 삽입/삭제 O(n) 만큼의 시간이 걸리는 연산

 

#include <iostream>
using namespace std;

class DynamicArray {
private:
// Pointer to store array created
// using new keyword
int* array = NULL;
// Size of array
int size;

// Container size
int capacity;

public:
// Default constructor with size 1
DynamicArray()
{
capacity = 1;
size = 0;
array = new int[capacity];
}

// Taking size from the user
DynamicArray(int capacity)
{
this->capacity = capacity;
array = new int[capacity];
size = 0;
}

// Returns the size of Array
// i.e Total elements stored currently
int getSize() { return size; }

// Returns the size of container
int getCapacity() { return capacity; }

// Inserting element after last stored index
void push_back(int value)
{
// check is array having size to store element or
// not
if (size == capacity) {

// if not then grow the array by double
growArray();
}

// insert element
array[size] = value;
// increment the size or last_index+1
size++;
}

// Deleting element at last stored index
void pop_back()
{
// Replace the last index by 0
array[size - 1] = 0;

// Decrement the array size
size--;

// Reduce if the container half element of its
// capacity
if (size == (capacity / 2)) {
shrinkArray();
}
}

// Increase the array size by double of current capacity
void growArray()
{

// Creating new array of double size
int* temp = new int[capacity * 2];

capacity = capacity * 2;
// copy element of old array in newly created array
for (int i = 0; i < size; i++) {
temp[i] = array[i];
}

// Delete old array
delete[] array;

// Assign newly created temp array to original array
array = temp;
}

// Reduce the size of array by half
void shrinkArray()
{

// Creating new array of half size
capacity = size;
int* temp = new int[capacity];

// copy element of old array in newly created array
for (int i = 0; i < size; i++) {
temp[i] = array[i];
}

// Delete old array
delete[] array;

// Assign newly created temp array to original array
array = temp;
}

// Searching element in the given array
int search(int key)
{
for (int i = 0; i < size; i++) {
if (array[i] == key) {
// If element found return its index
return i;
}
}

// Return -1 if element not found;
return -1;
}

// Insert element at given index
void insertAt(int index, int value)
{
// check is array having size to store element or
// not
if (size == capacity) {

// if not then grow the array by double
growArray();
}

for (int i = size - 1; i >= index; i--) {
array[i + 1] = array[i];
}

array[index] = value;
size++;
}

// Delete element at given index
void deleteAt(int index)
{
for (int i = index; i < size; i++) {
array[i] = array[i + 1];
}

// Replace the last index by 0
array[size - 1] = 0;

// Decrement the array size
size--;

// Reduce if the container half element of its
// capacity
if (size == (capacity / 2)) {
shrinkArray();
}
}

// To Print Array
void printArrayDetails()
{
cout << "Elements of array : ";
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
cout << "No of elements in array : " << size
<< ", Capacity of array :" << capacity << endl;
}

bool isEmpty()
{
if (size == 0) {
return true;
}
else {
return false;
}
}
};

int main()
{
DynamicArray da;

da.push_back(1);
da.push_back(2);
da.push_back(3);
da.push_back(4);
da.push_back(5);
da.push_back(6);
da.push_back(7);
da.push_back(8);
da.push_back(9);
da.push_back(10);
da.push_back(11);

da.printArrayDetails();

da.shrinkArray();
cout << "\nCapacity of array after shrinking : "
<< da.getCapacity() << endl;

cout << "\nAfter inserting at index 3 " << endl;
da.insertAt(3, 50);
da.printArrayDetails();

cout << "\nAfter delete last element ";
da.pop_back();
da.printArrayDetails();

cout << "\nAfter deleting at index 3 ";
da.deleteAt(3);
da.printArrayDetails();

cout << "\nSearching 5 in array ";
int index = da.search(5);
if (index != -1) {
cout << "Element found at index : " << index << endl;
}
else {
cout << "Element not found " << endl;
}
return 0;
}

// This code is contributed by Aniket Tiwari

 

 

배열과 연결 리스트 비교

배열 - 랜덤접근 가능 O(1), 데이터 삽입/삭제 O(n), 컴파일 단계에 정적으로 stack 영역에 할당

연결 리스트 - 랜덤접근 불가능 O(n), 데이터 삽입/삭제 O(1), 실행 단계에 동적으로 heap 영역에 할당

요약 - 배열은 접근이 빠르고 삽입,삭제가 느림, 연결 리스트는 반대로 접근이 느리고 삽입,삭제가 빠름

 

 

연결 리스트 - 요소가 인접한 메모리 영역에 저장되지 않은 선형 데이터 구조 

 

 

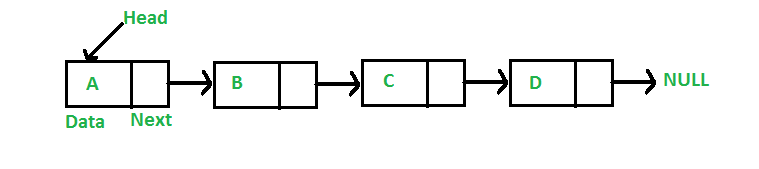
노드가 데이터와 다음 데이터의 주소를 가르키는 헤더로 이루어진 구조

 

단순 연결 리스트- 각 노드에 데이터와 포인터 1개씩, 포인터는 다음 노드
이중 연결 리스트 - 포인터 공간이 두개, 각각 포인터는 앞뒤 노드를 가르킴
원형 리스트 - 연결리스트의 마지막 노드가 처음 노드를 가르킴

 

장점

주소만 이어주면 되어서 중간 추가/삭제 O(1)

메모리가 동적으로 이루어져있기에 메모리 낭비가 없음

삽입, 삭제를 노드에 어느 지점에서든 가능

단점

랜덤 엑세스 불가, 순차 접근만 가능

각 노드마다 포인터를 위해 추가 메모리 공간이 필요함

특정 요소 탐색을 처음부터 진행하기에 O(n)의 시간이 걸림

 

연결 리스트 

 

이중 연결 리스트의 삽입 & 삭제

 

1)헤드 부분에 삽입

새 노드를 만들고 기존 헤드 노드의 prev가 새 노드값의 주소를 가르키게 하기

새 노드의 next에 기존 헤드 노드가 오게 하기

새 노드의 위치에 기존 헤드 노드를 넣고

헤드가 새 노드를 가르기케 함

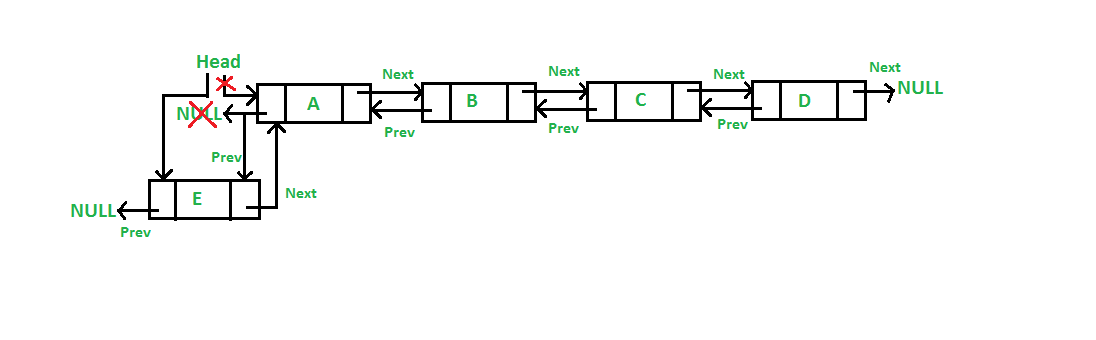
시간 복잡도 O(1)

/* Given a reference (pointer to pointer)
to the head of a list
and an int, inserts a new node on the
front of the list. */
void push(Node** head_ref, int new_data)
{
/* 1. allocate node */
Node* new_node = new Node();

/* 2. put in the data */
new_node->data = new_data;

/* 3. Make next of new node as head
and previous as NULL */
new_node->next = (*head_ref);
new_node->prev = NULL;

/* 4. change prev of head node to new node */
if ((*head_ref) != NULL)
(*head_ref)->prev = new_node;

/* 5. move the head to point to the new node */
(*head_ref) = new_node;
}

// This code is contributed by shivanisinghss2110

 

 

2) 이중 연결 리스트 중간에 삽입

기존 노드가 prev로 주어지고 새 노드가 기존 노드 뒤에 삽입하는 방식

새 노드의 next를 좌측 노드의 next로 변경

좌측 노드의 next가 새 노드를 가르키게 함

새 노드의 prev가 이전 노드를 가르키게 함

새 노드의 next 노드의 prev가 새 노트를 가르키게 함

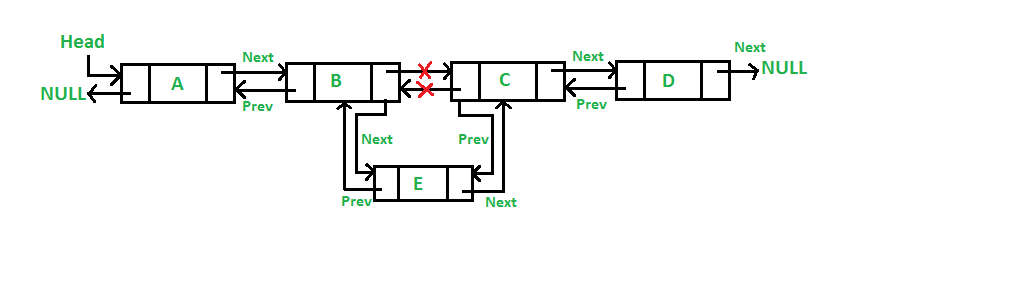
시간 복잡도 O(1)

/* Given a node as prev_node, insert
a new node after the given node */
void insertAfter(Node* prev_node, int new_data)
{
/*1. check if the given prev_node is NULL */
if (prev_node == NULL) {
cout << "the given previous node cannot be NULL";
return;
}

/* 2. allocate new node */
Node* new_node = new Node();

/* 3. put in the data */
new_node->data = new_data;

/* 4. Make next of new node as next of prev_node */
new_node->next = prev_node->next;

/* 5. Make the next of prev_node as new_node */
prev_node->next = new_node;

/* 6. Make prev_node as previous of new_node */
new_node->prev = prev_node;

/* 7. Change previous of new_node's next node */
if (new_node->next != NULL)
new_node->next->prev = new_node;
}

// This code is contributed by shivanisinghss2110.

3) 이중 연결 리스트 끝에 삽입

 

목록을 끝까지 탐색한 후에 마지막 노드를 찾아서 마지막 노드의 다음 노드를 새 노드로 변경하는 방법

새 노드를 할당하고 새 노드의 next를 null로 설정

인자로 받은 노드부터 노드의 next가 null인 끝 까지 순회

해당 위치에서 next에 새 노드를 넣어줌

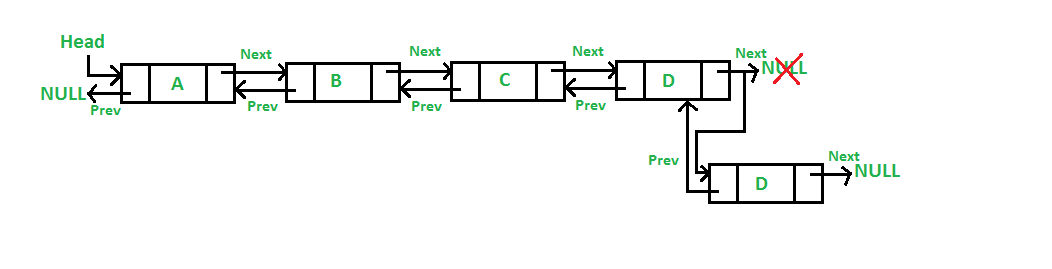
노드를 탐색을 해서 마지막 노드를 찾기에 시간복잡도 O(n)

/* Given a reference (pointer to pointer) to the head
of a DLL and an int, appends a new node at the end */
void append(Node** head_ref, int new_data)
{
/* 1. allocate node */
Node* new_node = new Node();

Node* last = *head_ref; /* used in step 5*/

/* 2. put in the data */
new_node->data = new_data;

/* 3. This new node is going to be the last node, so
make next of it as NULL*/
new_node->next = NULL;

/* 4. If the Linked List is empty, then make the new
node as head */
if (*head_ref == NULL) {
new_node->prev = NULL;
*head_ref = new_node;
return;
}

/* 5. Else traverse till the last node */
while (last->next != NULL)
last = last->next;

/* 6. Change the next of last node */
last->next = new_node;

/* 7. Make last node as previous of new node */
new_node->prev = last;

return;
}

// This code is contributed by shivanisinghss2110

 

4) 삭제

 

삭제할 노드가 헤드 노드인 경우와 아닌 경우 두가지

헤드 노드인 경우에는 다음 노드를 헤드로 만들고

노드가 삭제되면 삭제된 노드의 이전 노드와 다음 노드를 연결

 

순회하거나 새로운 공간을 필요로 하지는 않기에 

시간 복잡도, 공간 복잡도둘다 O(1)

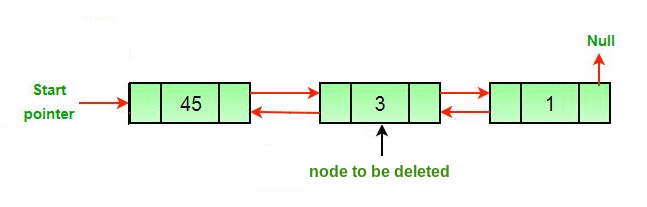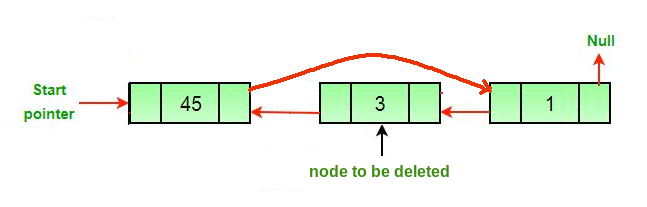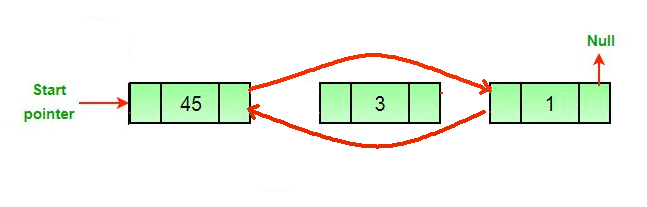
// C++ program to delete a node from
// Doubly Linked List
#include <bits/stdc++.h>
using namespace std;

/* a node of the doubly linked list */
class Node
{
public:
int data;
Node* next;
Node* prev;
};

/* Function to delete a node in a Doubly Linked List.
head_ref --> pointer to head node pointer.
del --> pointer to node to be deleted. */
void deleteNode(Node** head_ref, Node* del)
{
/* base case */
if (*head_ref == NULL || del == NULL)
return;

/* If node to be deleted is head node */
if (*head_ref == del)
*head_ref = del->next;

/* Change next only if node to be
deleted is NOT the last node */
if (del->next != NULL)
del->next->prev = del->prev;

/* Change prev only if node to be
deleted is NOT the first node */
if (del->prev != NULL)
del->prev->next = del->next;

/* Finally, free the memory occupied by del*/
free(del);
return;
}

/* UTILITY FUNCTIONS */
/* Function to insert a node at the
beginning of the Doubly Linked List */
void push(Node** head_ref, int new_data)
{
/* allocate node */
Node* new_node = new Node();

/* put in the data */
new_node->data = new_data;

/* since we are adding at the beginning,
prev is always NULL */
new_node->prev = NULL;

/* link the old list of the new node */
new_node->next = (*head_ref);

/* change prev of head node to new node */
if ((*head_ref) != NULL)
(*head_ref)->prev = new_node;

/* move the head to point to the new node */
(*head_ref) = new_node;
}

/* Function to print nodes in a given doubly linked list
This function is same as printList() of singly linked list */
void printList(Node* node)
{
while (node != NULL)
{
cout << node->data << " ";
node = node->next;
}
}

/* Driver code*/
int main()
{
/* Start with the empty list */
Node* head = NULL;

/* Let us create the doubly linked list 10<->8<->4<->2 */
push(&head, 2);
push(&head, 4);
push(&head, 8);
push(&head, 10);

cout << "Original Linked list ";
printList(head);

/* delete nodes from the doubly linked list */
deleteNode(&head, head); /*delete first node*/
deleteNode(&head, head->next); /*delete middle node*/
deleteNode(&head, head->next); /*delete last node*/

/* Modified linked list will be NULL<-8->NULL */
cout << "\nModified Linked list ";
printList(head);

return 0;
}

// This code is contributed by rathbhupendra

스택
LIFO (Last In First Out) / FILO (First In Last Out) 

마지막에 들어간 데이터가 먼저 나오는 선형 자료구조

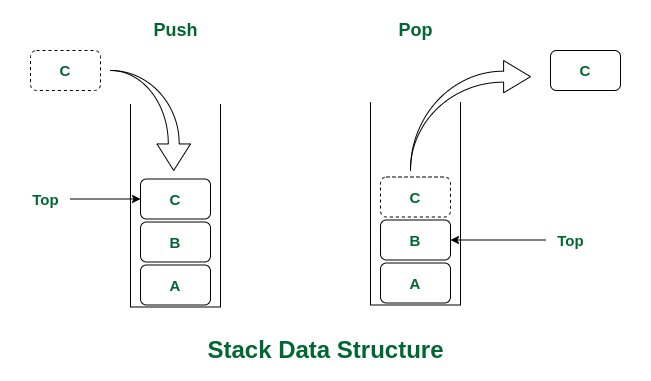
스택에서의 작업

 

스택에 요소를 삽입하는 push()
스택에서 요소를 제거하고 해당 요소를 반환하는 pop()

스택에서 요소를 제거하지 않고 최상단 요소를 반환하는 peek()
스택의 맨 위 요소를 반환하는 top()
스택이 비어 있는지 판단하는 isEmpty()
 스택의 크기를 반환하는 size()

 

삽입/삭제 O(1), 탐색에 O(n)의 시간이 소요

 

스택의 구현 - 배열이나 연결리스트로 구현됨

배열을 사용한 스택 구현

포인터를 사용하지 않으므로 메모리가 절약되나 정적임, 실행시 크기 변경 불가능

동적 배열을 사용하면 크기 조절 가능

/* C++ program to implement basic stack
operations */
#include <bits/stdc++.h>

using namespace std;

#define MAX 1000

class Stack {
int top;

public:
int a[MAX]; // Maximum size of Stack

Stack() { top = -1; }
bool push(int x);
int pop();
int peek();
bool isEmpty();
};

bool Stack::push(int x)
{
if (top >= (MAX - 1)) {
cout << "Stack Overflow";
return false;
}
else {
a[++top] = x;
cout << x << " pushed into stack\n";
return true;
}
}

int Stack::pop()
{
if (top < 0) {
cout << "Stack Underflow";
return 0;
}
else {
int x = a[top--];
return x;
}
}
int Stack::peek()
{
if (top < 0) {
cout << "Stack is Empty";
return 0;
}
else {
int x = a[top];
return x;
}
}

bool Stack::isEmpty()
{
return (top < 0);
}

// Driver program to test above functions
int main()
{
class Stack s;
s.push(10);
s.push(20);
s.push(30);
cout << s.pop() << " Popped from stack\n";

//print top element of stack after popping
cout << "Top element is : " << s.peek() << endl;

//print all elements in stack :
cout <<"Elements present in stack : ";
while(!s.isEmpty())
{
// print top element in stack
cout << s.peek() <<" ";
// remove top element in stack
s.pop();
}

return 0;
}

 

연결 리스트를 사용한 스택 구현

실행후 확장/축소 가능

랜덤 액세스는 연결 리스트로 만들었기에 불가능하다

// C++ program for linked list implementation of stack
#include <bits/stdc++.h>
using namespace std;

// A structure to represent a stack
class StackNode {
public:
int data;
StackNode* next;
};

StackNode* newNode(int data)
{
StackNode* stackNode = new StackNode();
stackNode->data = data;
stackNode->next = NULL;
return stackNode;
}

int isEmpty(StackNode* root)
{
return !root;
}

void push(StackNode** root, int data)
{
StackNode* stackNode = newNode(data);
stackNode->next = *root;
*root = stackNode;
cout << data << " pushed to stack\n";
}

int pop(StackNode** root)
{
if (isEmpty(*root))
return INT_MIN;
StackNode* temp = *root;
*root = (*root)->next;
int popped = temp->data;
free(temp);

return popped;
}

int peek(StackNode* root)
{
if (isEmpty(root))
return INT_MIN;
return root->data;
}

// Driver code
int main()
{
StackNode* root = NULL;

push(&root, 10);
push(&root, 20);
push(&root, 30);

cout << pop(&root) << " popped from stack\n";

cout << "Top element is " << peek(root) << endl;

cout <<"Elements present in stack : ";
//print all elements in stack :
while(!isEmpty(root))
{
// print top element in stack
cout << peek(root) <<" ";
// remove top element in stack
pop(&root);
}

return 0;
}

// This is code is contributed by rathbhupendra

스택 사용 예시 - undo, 백트래킹, 뒤로가기, 후위표기법, 역순 출력

 

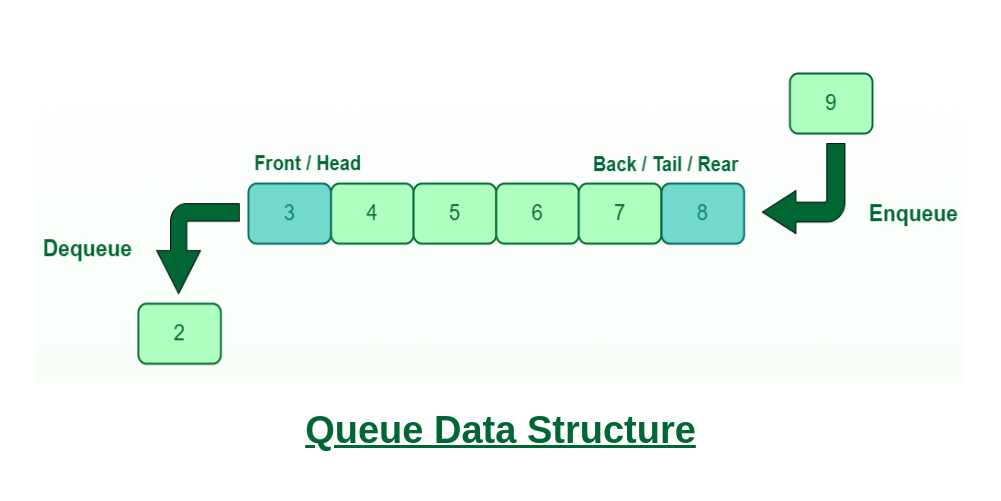
큐 - FIFO

한쪽에서는 데이터 삽입, 한쪽에서는 데이터 삭제가 이루어지는 자료구조

 

#include <iostream>

using namespace std;

// 노드 구조체
struct Node {
    int data;
    Node* next;
};

// 큐 클래스
class Queue {
private:
    Node* front;  // 큐의 맨 앞 노드를 가리키는 포인터
    Node* rear;  // 큐의 맨 뒤 노드를 가리키는 포인터

public:
    // 생성자
    Queue() {
        front = NULL;
        rear = NULL;
    }

    // enqueue
    void enqueue(int item) {
        Node* new_node = new Node;
        new_node->data = item;
        new_node->next = NULL;

        // 큐가 비어있는 경우
        if (rear == NULL) {
            front = new_node;
            rear = new_node;
        }
        // 큐가 비어있지 않은 경우
        else {
            rear->next = new_node;
            rear = new_node;
        }
    }

    // dequeue
    int dequeue() {
        // 큐가 비어있는 경우
        if (front == NULL) {
            cout << "Queue is empty!" << endl;
            return -1;
        }
        // 큐가 비어있지 않은 경우
        else {
            int data = front->data;
            Node* temp = front;
            front = front->next;
            delete temp;
            // 마지막 노드를 삭제한 경우 rear도 NULL로 초기화
            if (front == NULL) {
                rear = NULL;
            }
            return data;
        }
    }

    // is_empty
    bool is_empty() {
        return (front == NULL);
    }
};

int main() {
    Queue q;

    // enqueue
    q.enqueue(1);
    q.enqueue(2);
    q.enqueue(3);

    // dequeue
    cout << q.dequeue() << endl;  // 1
    cout << q.dequeue() << endl;  // 2

    // enqueue
    q.enqueue(4);

    // dequeue
    cout << q.dequeue() << endl;  // 3
    cout << q.dequeue() << endl;  // 4

    // dequeue (비어있는 큐에서 dequeue 시도)
    cout << q.dequeue() << endl;  // Queue is empty! / -1

    // is_empty
    cout << q.is_empty() << endl;  // 1 (true)
    return 0;
}

 

enqueue - 맨 끝에 데이터 추가
dequeue - 맨 앞에서 요소 제거
front - 자료가 삭제되는 영역

rear - 자료가 삽입되는 영역

스택과 큐의 차이점

 

스택은 한 방향으로만 접근할 수 있음,  후입 선출 구조
top을 통해서 push, pop을 하면서 삽입과 삭제
DFS나 재귀에서 사용된다.

큐는 한쪽 끝에서 삽입 작업을, 다른 쪽 끝에서 삭제 작업을 진행,선입선출 구조이다
데이터를 입력한 순서대로 처리할때 사용한다.
BFS나 캐시를 구현할 때 사용한다.

 

장점

삽입/삭제 연산 용의

여러 사용자가 사용할때 유용

 

단점

중간 요소 삽입/삭제는 O(n)의 시간이 걸림

빈 공간을 사용하려면 모든 자료를 꺼내거나 자료를 한 칸씩 옮겨야 함

 

 

 

원형 큐

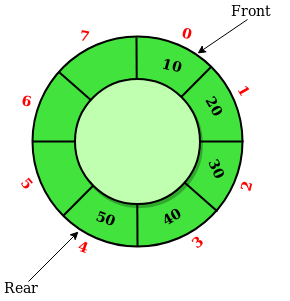
원형 큐 - 선형 큐의 처음과 끝을 연결

rear 와 front가 같은 공백 상태에서 시작

초기화시 rear와 front를 둘다 0으로 초기화

데이터 추가할땐 rear를 증가시키고 데이터를 증가시킨 rear인덱스 영역에 할당

데이터 삭제핼땐 front를 증가시키고 front 인덱스의 데이터를 삭제

 

#include <iostream>
using namespace std;

const int MAX_QUEUE_SIZE = 5;

class CircularQueue {
private:
    int front, rear;
    int data[MAX_QUEUE_SIZE];
public:
    CircularQueue() {
        front = rear = 0;
    }
    bool is_empty() {
        return front == rear;
    }
    bool is_full() {
        return (rear + 1) % MAX_QUEUE_SIZE == front;
    }
    void enqueue(int item) {
        if (is_full()) {
            cout << "Queue is full" << endl;
            return;
        }
        rear = (rear + 1) % MAX_QUEUE_SIZE;
        data[rear] = item;
    }
    int dequeue() {
        if (is_empty()) {
            cout << "Queue is empty" << endl;
            return -1;
        }
        front = (front + 1) % MAX_QUEUE_SIZE;
        return data[front];
    }
    void display() {
        cout << "Queue: ";
        if (!is_empty()) {
            int i = (front + 1) % MAX_QUEUE_SIZE;
            do {
                cout << data[i] << " ";
                i = (i + 1) % MAX_QUEUE_SIZE;
            } while (i != (rear + 1) % MAX_QUEUE_SIZE);
        }
        cout << endl;
    }
};

int main() {
    CircularQueue q;

    q.enqueue(1);
    q.enqueue(2);
    q.enqueue(3);
    q.enqueue(4);
    q.enqueue(5);  // 큐가 가득 참

    q.display();

    q.dequeue();
    q.dequeue();
    q.enqueue(6);
    q.enqueue(7);

    q.display();

    return 0;
}

 

큐 사용 예시

 순서대로 작업,데이터를 실행,대기 시킬때 사용
비동기 전송, 자료를 일시적으로 저장할때 사용

 

 

deque(double-ended queue)

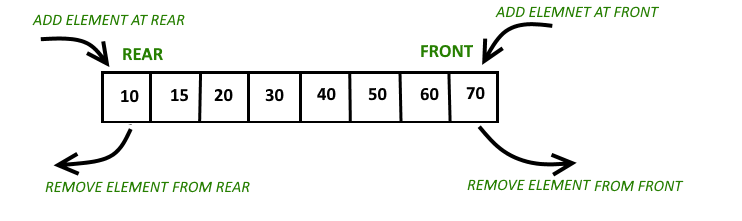
양쪽 끝에서 삽입과 삭제가 모두 가능한 자료구조, 스택과 큐의 기능을 모두 갖고 있음

웹 브라우저의 기록,  프로그램의 실행 취소 작업 목록 저장 등에 사용

 

push_back : deque의 뒷 부분에 원소 추가
push_front : deque의 앞 부분에 원소 추가
pop_back : deque의 뒷 부분 원소 삭제
pop_front : deque의 앞 부분 원소 삭제

front : 앞 부분 가져오기

back : 뒷 부분 뒷 부분 가져요기

 

배열을 이용한 deque 구현

// C++ implementation of De-queue using circular
// array
#include <iostream>
using namespace std;

// Maximum size of array or Dequeue
#define MAX 100

// A structure to represent a Deque
class Deque {
int arr[MAX];
int front;
int rear;
int size;

public:
Deque(int size)
{
front = -1;
rear = 0;
this->size = size;
}

// Operations on Deque:
void insertfront(int key);
void insertrear(int key);
void deletefront();
void deleterear();
bool isFull();
bool isEmpty();
int getFront();
int getRear();
};

// Checks whether Deque is full or not.
bool Deque::isFull()
{
return ((front == 0 && rear == size - 1)
|| front == rear + 1);
}

// Checks whether Deque is empty or not.
bool Deque::isEmpty() { return (front == -1); }

// Inserts an element at front
void Deque::insertfront(int key)
{
// check whether Deque if full or not
if (isFull()) {
cout << "Overflow\n" << endl;
return;
}

// If queue is initially empty
if (front == -1) {
front = 0;
rear = 0;
}

// front is at first position of queue
else if (front == 0)
front = size - 1;

else // decrement front end by '1'
front = front - 1;

// insert current element into Deque
arr[front] = key;
}

// function to inset element at rear end
// of Deque.
void Deque ::insertrear(int key)
{
if (isFull()) {
cout << " Overflow\n " << endl;
return;
}

// If queue is initially empty
if (front == -1) {
front = 0;
rear = 0;
}

// rear is at last position of queue
else if (rear == size - 1)
rear = 0;

// increment rear end by '1'
else
rear = rear + 1;

// insert current element into Deque
arr[rear] = key;
}

// Deletes element at front end of Deque
void Deque ::deletefront()
{
// check whether Deque is empty or not
if (isEmpty()) {
cout << "Queue Underflow\n" << endl;
return;
}

// Deque has only one element
if (front == rear) {
front = -1;
rear = -1;
}
else
// back to initial position
if (front == size - 1)
front = 0;

else // increment front by '1' to remove current
// front value from Deque
front = front + 1;
}

// Delete element at rear end of Deque
void Deque::deleterear()
{
if (isEmpty()) {
cout << " Underflow\n" << endl;
return;
}

// Deque has only one element
if (front == rear) {
front = -1;
rear = -1;
}
else if (rear == 0)
rear = size - 1;
else
rear = rear - 1;
}

// Returns front element of Deque
int Deque::getFront()
{
// check whether Deque is empty or not
if (isEmpty()) {
cout << " Underflow\n" << endl;
return -1;
}
return arr[front];
}

// function return rear element of Deque
int Deque::getRear()
{
// check whether Deque is empty or not
if (isEmpty() || rear < 0) {
cout << " Underflow\n" << endl;
return -1;
}
return arr[rear];
}

// Driver code
int main()
{
Deque dq(5);

// Function calls
cout << "Insert element at rear end : 5 \n";
dq.insertrear(5);

cout << "insert element at rear end : 10 \n";
dq.insertrear(10);

cout << "get rear element "
<< " " << dq.getRear() << endl;

dq.deleterear();
cout << "After delete rear element new rear"
<< " become " << dq.getRear() << endl;

cout << "inserting element at front end \n";
dq.insertfront(15);

cout << "get front element "
<< " " << dq.getFront() << endl;

dq.deletefront();

cout << "After delete front element new "
<< "front become " << dq.getFront() << endl;
return 0;
}