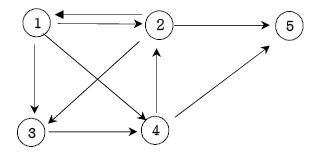
위 그림같은 방향 그래프를 1번부터 시작해서 5번까지 가는 방법의 갯수를 구해보자
인접행렬은 for문, 인접리스트는 foreach문을 사용, 인접리스트 처음에 생성할때 i = 0; i <= m ; i++
인접 행렬
방문한 노드를 체크할 배열과, 한 노드가 방문할수 있는 다른 노드들을 체크할 2차원 배열을 만들고 방문 가능한 노드들을 채워준다
for (int i = 0; i < m; i++){
int a = in.nextInt();
int b = in.nextInt();
graph[a][b]= 1;
}dfs 함수에서는 노드 길이만큼 for문을 돌면서 현재 정점에서 방문 가능한 노드이고 간 적이 없으면 그 노드를 방문한다
목적지 노드까지 도달하면 갯수를 늘려준다, 한 노드를 방문할땐 방문여부를 체크하고 다시 뒤로 돌아올땐 체크를 푼다.
public int dfs(int v){
if (v == n) ans++;
else {
for (int i = 1; i <= n; i++){
//현재 정점에서 for문으로 n번 노드중 갈 수 있는 노드 찾기
if(graph[v][i] == 1 && ch[i] == 0){
ch[i] = 1;
dfs(i);
ch[i] = 0;
}
}
}
return ans;
}
인접행렬 경로탐색 전체 코드
import java.util.*;
public class Main{
static int n,m,ans = 0;
static int[][] graph;
static int[] ch;
public int dfs(int v){
if (v == n) ans++;
else {
for (int i = 1; i <= n; i++){
//현재 정점에서 for문으로 n번 노드중 갈 수 있는 노드 찾기
if(graph[v][i] == 1 && ch[i] == 0){
ch[i] = 1;
dfs(i);
ch[i] = 0;
}
}
}
return ans;
}
public static void main(String args[]) {
Main T = new Main();
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
graph = new int[n+1][n+1];
ch = new int[n+1];
//그래프의 a -> b 방향으로 방문 가능한 곳을 채워둠
for (int i = 0; i < m; i++){
int a = in.nextInt();
int b = in.nextInt();
graph[a][b]= 1;
}
ch[1] = 1;
System.out.print(T.dfs(1));
}
}
ArrayList로 경로 탐색
인접행렬로는 n이 커지면 너무 비효율적이다
1~n을 가지는 배열리스트를 만들고해당 정점에서 갈 수 있는 노드를 리스트에 추가, 탐색한다
1 | 2, 3, 4
2 | 1, 3, 5
3 | 4
4 | 2, 5
5
위 형태로 ArrayList 안에 각 노드 번호의 ArrayList를 만들고 각 노드에서 한번만에 갈 수 있는 노드들을
추가해준다, 이걸 위해서 ArrayList안에 ArrayList를 가진 형태로 그래프를 만들어준다
static ArrayList<ArrayList<Integer>>graph;
arraylist를 가지는 arraylist 객체
get으로 ArrayList의 인덱스를 가져올때 0번부터 시작하므로 0번부터 n번까지 진행해서 앞에 한칸을 추가해 인덱스를 맞춰준다
// 정점개수 n 만큼 그래프에 배열리스트 추가
// 중요! 0부터 n까지 하는 이유는 get으로 인덱스를 조회할때 0번부터 시작하기 때문에
// 앞에 한칸을 더 해줘야 인덱스에 딱 맞게 추가 가능하다
for(int i = 0; i <=n; i++) {
graph.add(new ArrayList<Integer>());
}위의 그린 그림대로 방문 가능한 정점을 추가한다
for (int i = 0; i < m; i++){
int a = in.nextInt();
int b = in.nextInt();
//위에 만든 인덱스에 맞는 배열 리스트에 방문 가능한 정점을 추가
graph.get(a).add(b);
}인접 리스트 DFS 함수는 foreach문으로 해당 인덱스 노드에서 갈수 있는 노드를 순회한다
public void dfs(int v){
if (v == n) ans++;
else {
//현재 정점에서 foreach문으로 n번 노드중 갈 수 있는 노드 찾기
for (int nv : graph.get(v)){
if(ch[nv] == 0){
ch[nv] = 1;
dfs(nv);
ch[nv] = 0;
}
}
}
}인접 리스트 경로 탐색 전체 코드
import java.util.*;
public class Main{
static int n,m,ans = 0;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch;
public void dfs(int v){
if (v == n) ans++;
else {
//현재 정점에서 foreach문으로 n번 노드중 갈 수 있는 노드 찾기
for (int nv : graph.get(v)){
if(ch[nv] == 0){
ch[nv] = 1;
dfs(nv);
ch[nv] = 0;
}
}
}
}
public static void main(String args[]) {
Main T = new Main();
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
graph = new ArrayList<ArrayList<Integer>>();
// 정점개수 n 만큼 그래프에 배열리스트 추가
// 중요! 0부터 n까지 하는 이유는 get으로 인덱스를 조회할때 0번부터 시작하기 때문에 앞에 한칸을 더 해줘야 인덱스에 딱 맞게 추가 가능하다
for(int i = 0; i <=n; i++) {
graph.add(new ArrayList<Integer>());
}
ch = new int[n+1];
for (int i = 0; i < m; i++){
int a = in.nextInt();
int b = in.nextInt();
//위에 만든 인덱스에 맞는 배열 리스트에 방문 가능한 정점을 추가
graph.get(a).add(b);
}
ch[1] = 1;
T.dfs(1);
System.out.println(ans);
}
}'알고리즘 이전 > 재귀, DFS, BFS, Tree, Graph' 카테고리의 다른 글
| 합이 같은 부분집합 (0) | 2023.08.23 |
|---|---|
| 그래프 최단거리(BFS) (0) | 2023.08.18 |
| 말단 노드까지의 가장 짧은 경로 (0) | 2023.08.16 |
| 송아지 찾기(BFS) (0) | 2023.08.15 |
| 레벨 탐색(BFS) (0) | 2023.08.15 |

